데이터셋 : sklearn 패키지에 포함된 보스턴 주택 가격

0. 라이브러리 임포트
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.datasets import load_boston
1. 데이터셋 불러오기
boston = load_boston()
bostonDF = pd.DataFrame(boston.data, columns = boston.feature_names)boston 데이터를 불러오고
데이터프레임 형식으로 바꿔준다.
2. 타겟 컬럼 지정
bostonDF['PRICE'] = boston.target
bostonDF주택의 가격을 타겟 컬럼으로 지정

3. 각 컬럼별로 주택 가격에 대한 미치는 영향을 시각화
flg, axs = plt.subplots(figsize=(16,8), ncols = 4, nrows =2) # 한 행에 4개씩 두 행에 빈 그래프를 그려줌
im_features = ['RM','ZN','INDUS','NOX','AGE','PTRATIO','LSTAT','RAD']
for i, feature in enumerate(im_features):
#subplot으로 만들어준 빈 그래프에 순서대로 하나씩 채워줌.
# i = 0 -> 0/4 = 0 , 0%0 = 0 RM 0...0...0...1
# i = 1 -> int(1/4) = 0 , 1%4 = 1 ZN ...... 2... 3....
row = int(i/4)
col = i%4
# regplot은 산점도와 회귀선을 같이 그려준다.
sns.regplot(x = feature, y='PRICE', data = bostonDF, ax = axs[row][col])
#x 값은 피쳐들을 넣어주고 y 값은 price를 넣어줘서 각 피쳐들과 price의 회귀 선형회귀를 볼 수 있다.- subplots으로 빈 그래프를 4 x 2 만큼 그려준다.
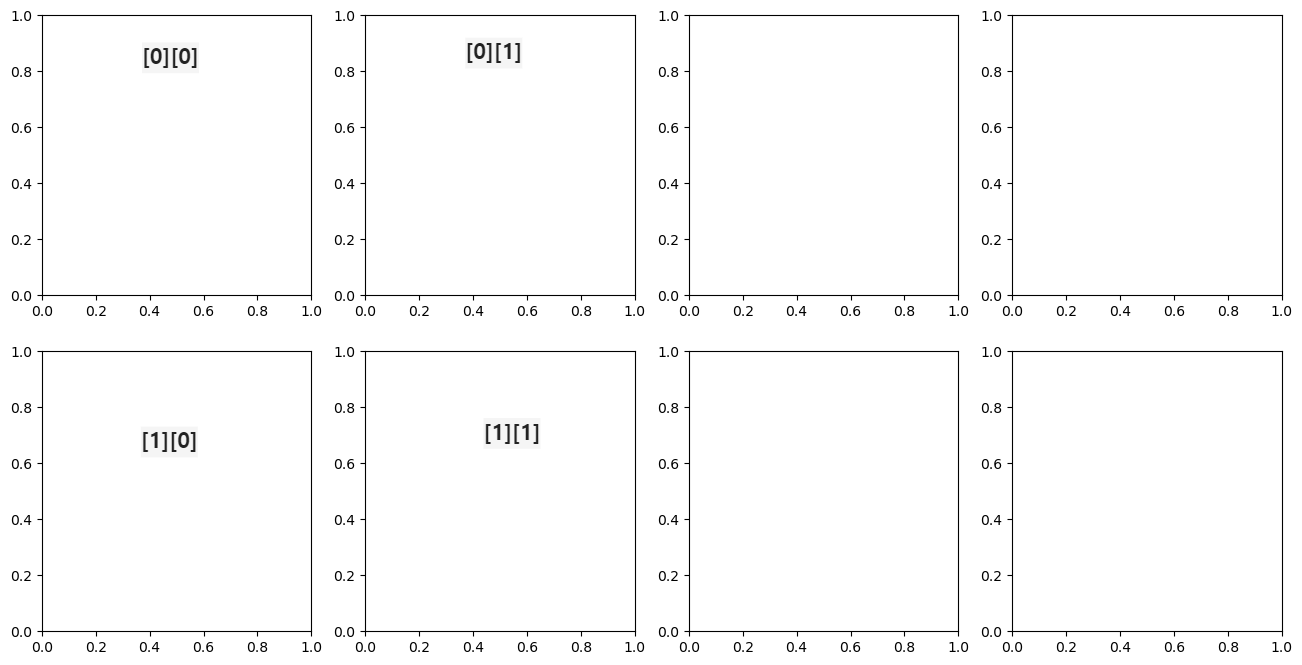
- 피쳐들을 리스트 형식으로 뽑아주고 for문을 통해서 RM ~ RAD까지 하나씩 그래프를 채운다.
- for문은 i가 0이 들어가면 row = 0, col = 0 이 되어서 axs[0][0] 이 된다. -> RM은 [0][0] 자리에 그려짐.
- row는 i = 4 가 되는 시점부터 int(i/4) 가 1이 되면서 두 번째 행의 그래프가 채워진다.
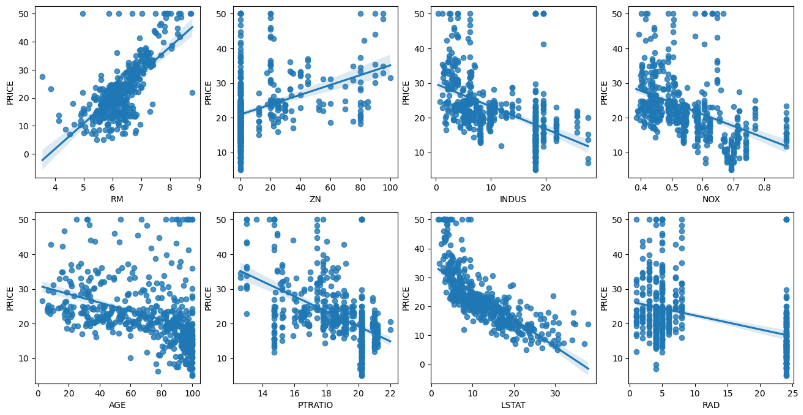
- LSTAT(하위계층비율)이 높을 수록 집값 또한 크게 떨어지는 추세를 보인다. (자본주의는 차갑다..)
4. 데이터셋 분리
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error, r2_score
# 데이터셋 분리
y_target = bostonDF['PRICE'] # 종속변수 PRICE만 추출해서 y
X_data = bostonDF.drop(['PRICE'], axis = 1, inplace = False) # df에서 PRICE만 제외하고 X
X_train, X_test, y_train, y_test = train_test_split(X_data, y_target, test_size = 0.3, random_state = 156)이번에도 사이킷런의 모델 셀렉션을 이용해서 피쳐와 타겟을 분리
타겟은 DF의 가격만 추출해서 넣어주고 피쳐는 DF의 PRICE를 제외하고 할당 axis = 1
훈련셋과 테스트셋의 비율윤 0.3으로 해주었다.
5. 학습 및 모델 성능 평가
reg = LinearRegression() # 선형회귀 모델 객체 생성
reg.fit(X_train,y_train) # 훈련셋으로 학습
y_pred = reg.predict(X_test) # X_test 값에 대한 예측값을 y_pred에 저장
mse = mean_squared_error(y_test, y_pred)
rmse = np.sqrt(mse) # mse에 루트
# MSE = 오차 제곱의 합 , RMSE = MSE에 루트
print('MSE : {0:.3f}, RMSE : {1:.3f}'.format(mse,rmse))
print('Variance score: {0:.3f}'.format(r2_score(y_test,y_pred)))선형회귀 객체를 생성하고, 학습을 시켜준다.
y_pred에 X_test에 대한 예측값을 넣어주고 mse와 rmse를 구해준다.

6. 마무리
print('절편값 :',reg.intercept_)
print('회귀 계수 값 :',np.round(reg.coef_,1)) # 각 피쳐들의 회귀 계수절편값(intercept_)과 회귀 계수 값(coef_)를 구해준다.

절편값과 회귀 계수 값이 이렇게 나오는데 피쳐들과 회귀 계수 값을 매핑시켜 주는 작업이 필요하다.
coeff = pd.Series(data = np.round(reg.coef_,1), index = X_data.columns)
coeff.sort_values(ascending=False)회귀 계수 값들을 시리즈 형태로 저장한다.
data = 는 coef를 라운드처리한 것으로 넣어주고, 인덱스는 피쳐들의 컬럼을 가져온다.

NOX는 오버피팅 ??? 추가적으로 찾아봐야겠다.
'데이터 분석 > MLDL' 카테고리의 다른 글
| 배깅과 부스팅 (0) | 2024.02.20 |
|---|---|
| Feature Selection에 대해 (0) | 2024.02.13 |
| [머신러닝 기초] 분류 모델 평가 지표 등등 (1) | 2024.02.08 |
| 로지스틱 회귀 간단 실습 (0) | 2024.01.30 |
| 선형 회귀 기초 - 공부 시간에 따른 시험 점수 (0) | 2024.01.26 |
