시계열 데이터
시계열 데이터란 시간에 따라 순차적으로 관측되는 데이터의 집합을 의미한다.
시계열 데이터 분석은 정상성을 가정하고 진행한다.
정상성이란 통계적 속성(평균, 분산)이 시간에 따라 일정한 것을 의미

왼쪽 그림은 시간이 지남에 따라 상승하는 추세가 있고, 계절성이 있어 보인다. 즉, 정상성 x
오른쪽 그림은 평균이 0 근처이며 분산 역시 어느 정도 일정한 모습을 보인다. 정상성 o
더빈 왓슨 검정

from statsmodels.stats.stattools import durbin_watson
dw_result = durbin_watson(df['Close'].values.squeeze())
print(f"Durbin-Watson statistic: {dw_result}")
-> 0.00028536925651245364이 값이 2에 가까우면 시계열 데이터에 자기상관이 없음을 나타냄. 반면에, 이 값이 0에 가까우면 자기상관이 있고
4에 가까우면 음의 자기상관이 있음을 의미한다.
ACF, PACF
자기상관과 편자기상관을 나타내는 그래프

위 애플 주가 데이터로 ACF, PACF 그래프를 그렸다.
왼쪽 그림은 ACF 그래프, 비정상 시계열로 자기상관이 크고 양수이며 천천히 감소하는 패턴을 가졌다.
오른쪽 그림은 PACF 그래프, 시차 1까지 높고 뚝 떨어지는? 모습을 보아 상관을 가지는 것을 알 수 있다.
보통 정상 시계열의 ACF는 상대적으로 빨리 0으로 접근하며
비정상 시계열의 ACF는 상대적으로 천천히 감소하며 종종 큰 양의 값을 가진다.
차분
위 애플 주가 데이터처럼 주가 데이터는 트렌드나 변동성 등으로 인해 정상성을 만족하지 않는 경우가 많다.
비정상 시계열로 학습을 하게 되면 모델이 복잡해지고 학습 난이도가 높아진다.
차분.. 해야겠지??
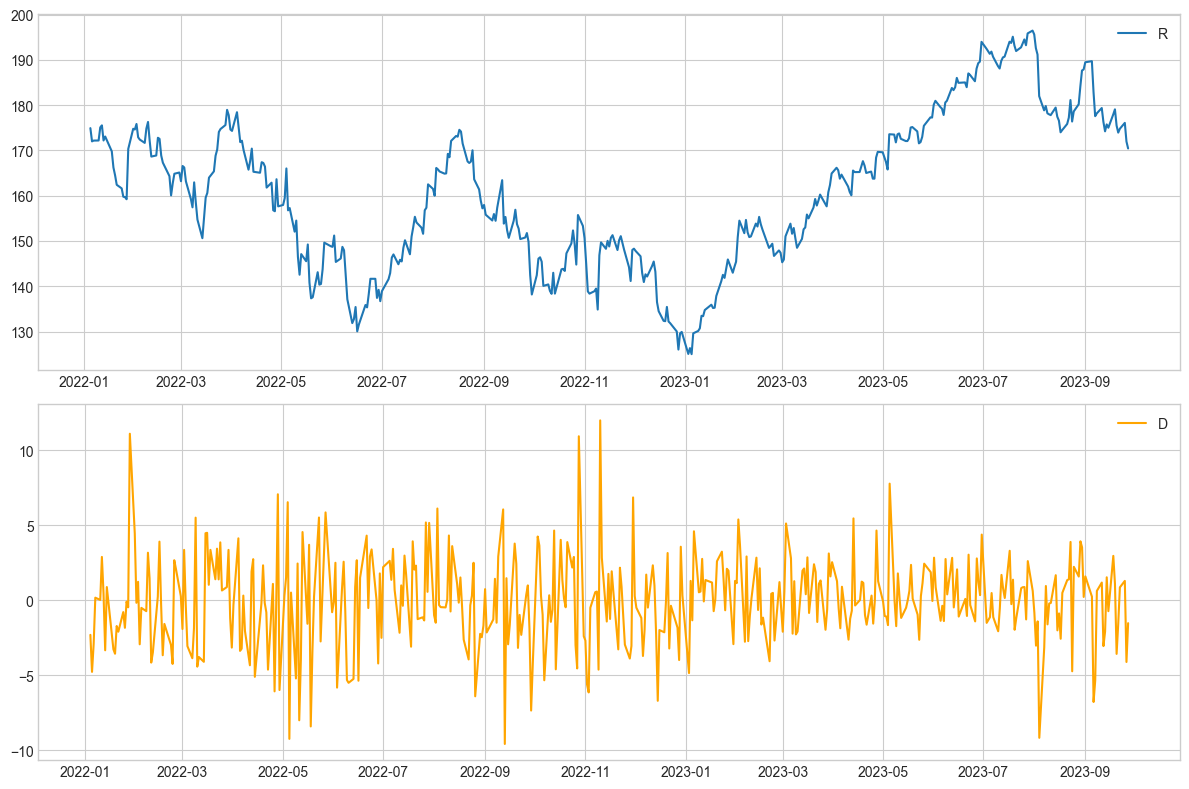
위 사진은 애플 주가 데이터를 1회 차분한 그래프다.
diff()로 간단하게 가능하며, 평균과 분산이 안정된 모습이다.

차분을 진행한 애플 주가 데이터의 ACF, PACF 그래프의 모습이다
lag(0) 지점 외 모든 시차에서 95% 신뢰구간을 벗어나지 않는다.
이 데이터로 더빈 왓슨 검정을 진행하면

2에 가까운 수치가 나온다. 위에서 말했듯이 이 값이 2에 가까우면 자기상관이 없음을 나타낸다.
아리마 모델에서 p와 q는 아래와 같이 결정한다. ARIMA(p,d,q)
ACF : 0이 되는 이전 시차가 q
PACF : 0이 되는 이전 시차가 p
대충 p와 q를 0으로 잡고 차분을 1회 진행 한 모델을 사용한다면 ARIMA(0,1,0)가 된다.
auto arima로 적합한 값을 찾을 수도 있다.
요악하자면
시계열 데이터의 예측은 정상성을 가정하고 진행한다.
ACF, PACF(편자기상관) 그래프는 시계열 데이터의 정상성을 평가하고
아리마 모델의 파라미터 결정 및 모델의 적합도 평가에 쓰인다.
변동폭이 일정하지 않으면 로그변환을 통해 분산이 일정하게 변환
추세나 계절적 요인이 관찰되면 차분을 통해 전 기간에 걸쳐 평균이 일정한 정상 시계열로 변환
변동폭이 일정하지 않고 추세와 계절적 요인 또한 존재한다면 로그변환과 차분과정을 모두 적용

(a)와 같이 시간에 따라 변동폭이 일정하지 않고 추세와 계절성이 있는 데이터를
로그변환 하게 되면 (b)와 같이 변동폭이 일정해진다.
차분을 하게 되면 (c)와 같이 평균이 일정하게 된다.
로그변환가 차분을 함께 진행하면 (d)와 같이 평균과 분산이 일정한 정상 시계열로 변환이 된다.
ARIMA vs Prophet
ARIMA
자기회귀(AR), 차분(I), 이동평균(MA) 세 가지 컴포넌트를 결합한 모데이다.
시계열 데이터가 정상 상태를 만족해야 하며, 만약 그렇지 않다면 차분을 통해 정상 시계열로 만들어야 한다.
계절성을 직접적으로 모델링하지 않으므로 계절성을 포함하는 SARIMA를 사용할 수도 있다.
선형성을 가정하며, 비선형 패턴을 잘 포착하지 못할 수도 있다.
1 - AR Model
Autoregressive(자기회귀) 모델은 과거 시점의 자기 자신의 데이터가 현시점의 자기 자신에게 영향을 미치는 모델이라는 뜻이다.
2 - MA Model
Moving Average(이동평균)모델은 트렌드(추세)가 변하는 상황에서 적합한 모델이다.
이전 상태의 자기자신을 보는 것이 아닌, 이전 항에서의 error텀을 현시점에 반영한다는 뜻이다.
추세를 반영해 추정한다는 뜻이다.
3 - ARMA Model
1- AR 과 2 - MA 모델을 합친 모델이다.
현재 시점의 상태를 파악하는 과거 시점의 자기 자신과 추세까지 모두 고려하겠다는 의미다.
4 - ARIMA Model
1~3 모델의 경우 시계열이 정상성이라는 가정을 기반으로 진행
ARIMA모델은 차분이라는 개념을 적용해 non-stationary 한 데이터를 더 잘 예측하는 것이 목표다.
위에서 말했듯이 ARIMA(p,d,q)에서 d가 차분을 의미한다.
결과 보고서

아리마 모델은 이러한 결과 보고서 기능을 제공하는데 해석하기가 어렵다...
우선 모델은 SARIMA(1,1,1) 모델이다.
AIC : 모델의 적합도와 복잡도를 균형 있게 고려하는 지표. 이 값이 작을수록 모델의 적합도가 높고, 모델의 복잡도가 낮다는 것을 나타낸다.
BIC : AIC와 비슷하지만, AIC와 달리 모델의 복잡도에 더 큰 페널티를 부여한다.
Ljung-Box (L1) (Q) : 잔차의 자기상관을 평가하는 검정으로, 이 모델에서는 1번째 시차에서 검정 통계량이 0.12이며,
p-value가 0.73이다. 이는 잔차의 자기상관이 없다는 가설을 지지한다.
Jarque-Bera (JB) 검정 : 잔차의 정규성을 평가하는 검정으로, 이 모델에서는 검정 통계량이 62.23이며 ,
p-value가 0.00이다. 이는 잔차가 정규분포를 따르지 않는다는 가설을 지지한다.
Heteroskedasticity (H) : 이분산성을 평가하는 검정, 0.45의 값이 나왔고 p-value가 0.00이다.
이는 잔차가 이분산성을 가진다는 가설을 지지한다.
Skeness(왜도), Kurtosis(첨도) : 왜도는 0.01로 거의 대칭에 가깝고, 첨도는 4.66으로 정규분포보다 뾰족한 형태를
가지고 있다.
종합적으로 SARIMA(1,1,1) 모델이 위 시계열 데이터에서 적합하다고 볼 수는 있지만, 잔차의 정규성과 이분산성에 대한 가정이 충족되지 않을 수 있으므로, 추가적인 검증과 모델 개선이 필요하다.
Prophet
선형 또는 비선형 경향성에 대한 유연성과 함께 계절성과 휴일 효과를 자동으로 모델링한다.
따라서 계절성, 휴일 패턴이 두드러지는 데이터에 효과적이다.
비정상 시계열 데이터에도 적용할 수 있으며, 데이터의 트렌드 변화를 자동으로 감지한다.
비선형성을 처리할 수 있으며, 더욱 복잡한 패턴을 포착할 수 있다.
계절성 : 특정 시점(분기 보고서 발표일, 연말 등) 주가가 일정한 패턴을 보이는 것을 계절성이라고 한다.
'데이터 분석 > MLDL' 카테고리의 다른 글
| K-Means(K-평균) 알고리즘 (3) | 2024.02.28 |
|---|---|
| 배깅과 부스팅 (0) | 2024.02.20 |
| Feature Selection에 대해 (0) | 2024.02.13 |
| [머신러닝 기초] 분류 모델 평가 지표 등등 (1) | 2024.02.08 |
| 선형회귀 연습 (0) | 2024.01.30 |
